TUBERIAS EN SERIE Y PARALELO CON SOLVER
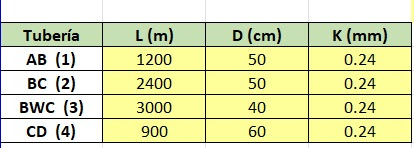
Ejercicio : Se tiene dos reservorios A y D, cuyos espejos de agua se ubican en las cotas +30 msnm y +21 msnm. Se tiene luego las tuberías AB, BC, BWC y CD cuyas características son las indicadas.Se pide determinar el caudal circulante en cada una de las tuberías.
SOLUCION :
Paso 01:Definir las ecuaciones que permiten analizar el sistema
Ecuaciones:
h1 + h2 + h4 = 9 m
h2=h3
Q1= Q2+Q3
Q1= Q4
Paso 02: Asumir los caudales que circulan por la tubería 1, 2, 3 y 4 en m3/s.(Rango de celdas B16:B19)
Paso 03:Determinamos el área para cada una de las tuberías.(Rango de celdas F16:F19)
A=3.1416D^2/4
Paso 04: Calculamos la velocidad .(Rango de celdas G16:G19)
V=Q/A
donde : V=velocidad en m/s
Q= caudal en m3/s
A= Area en m2
Paso 05: Calculamos el número de Reynolds.(Rango de celdas H16:H19)
Re = VD/visc
donde : Re = número de Reynolds
V=velocidad en m/s
D= diámetro de la tubería en m
Viscocidad cinemática = 10^-6 m2/s
Paso 06: Calculamos la pérdida de carga en cada tubería.
Darcy Weisbach hf = f L/D V^2/(2g)
donde : f = coeficiente de fricción de Darcy
L= longitud de la tubería en m
D= Diámetro de la tubería en m
k = Rugosidad absoluta de la tubería en m
El coeficiente de fricción de Darcy f: lo vamos a calcular con la fórmula de Barr
1/raiz(f) = -2 log(K/(3.7*D) + 5.1286/Re^0.89)
RHS=-2 log(K/(3.7*D) + 5.1286/Re^0.89)
f=1/RHS^2
- Calculamos el RHS (Rango de celdas I16:I19)
RHS=-2 log(K/(3.7*D) + 5.1286/Re^0.89)
- Calculamos el coeficiente de fricción de Darcy (Rango de celdas J16:J19)
f=1/RHS^2
- Calculamos la pérdida de carga en cada tubería. (Rango de celdas K16:K19)
Darcy Weisbach hf = f L/D V^2/(2g)
Paso 07: Definir las condiciones o restricciones.
h1 + h2 + h4 - 9 = 0
h2 - h3 = 0
Q1 - Q2 - Q3 = 0
Q1 - Q4 = 0
Paso 08: Definir el objetivo
El obetivo es la suma de todas las condiciones que para este caso debe ser cero.
RESULTADOS:









No hay comentarios.:
Publicar un comentario